一文教你用python编写Dijkstra算法进行机器人路径规划(算法节点)

为了机器人在寻路的过程中避障并且找到最短距离，我们需要使用一些算法进行路径规划（Path Planning），常用的算法有Djikstra算法、A*算法等等，在github上有一个非常好的项目叫做PythonRobotics，其中给出了源代码，参考代码，可以对Djikstra算法有更深的了解。

一、算法原理

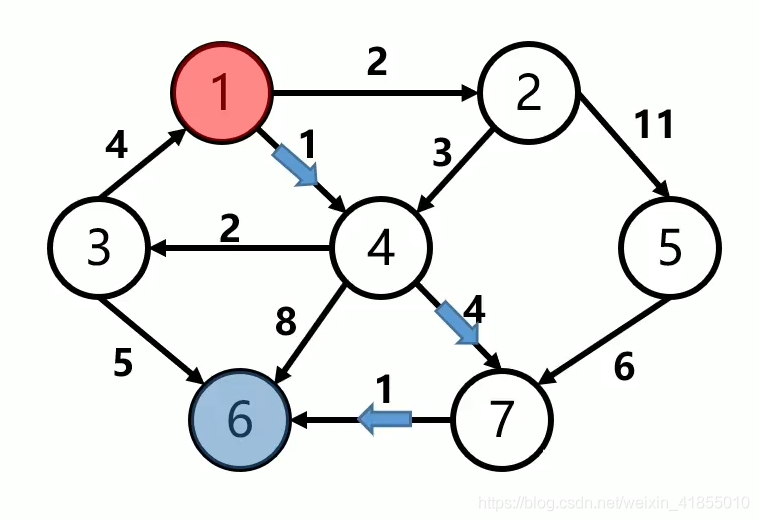
如图所示，Dijkstra算法要解决的是一个有向权重图中最短路径的寻找问题，图中红色节点1代表起始节点，蓝色节点6代表目标结点。箭头上的数字代表两个结点中的的距离，也就是模型中所谓的代价（cost）。

贪心算法需要设立两个集合，open_set（开集）和closed_set（闭集），然后根据以下程序进行操作：

把初始结点放入到open_set中；
把open_set中代价最小的节点取出来放入到closed_set中，并且作为当前节点；
把与当前节点相邻的节点放入到open_set中，如果代价更小更新代价
重复2-3过程，直到找到终点。

注意open_set中的代价是可变的，而closed_set中的代价已经是最小的代价了，这也是为什么叫做open和close的原因。

至于为什么closed_set中的代价是最小的，是因为我们使用了贪心算法，既然已经把节点加入到了close中，那么初始点到close节点中的距离就比到open中的距离小了，无论如何也不可能找到比它更小的了。

二、程序代码

"""
Grid based Dijkstra planning
author: Atsushi Sakai(@Atsushi_twi)
"""
import matplotlib.pyplot as plt
import math
show_animation = True

class Dijkstra:
 def __init__(self, ox, oy, resolution, robot_radius):
  """
  Initialize map for a star planning
  ox: x position list of Obstacles [m]
  oy: y position list of Obstacles [m]
  resolution: grid resolution [m]
  rr: robot radius[m]
  """
  self.min_x = None
  self.min_y = None
  self.max_x = None
  self.max_y = None
  self.x_width = None
  self.y_width = None
  self.obstacle_map = None
  self.resolution = resolution
  self.robot_radius = robot_radius
  self.calc_obstacle_map(ox, oy)
  self.motion = self.get_motion_model()
 class Node:
  def __init__(self, x, y, cost, parent_index):
self.x = x  # index of grid
self.y = y  # index of grid
self.cost = cost
self.parent_index = parent_index  # index of previous Node
  def __str__(self):
return str(self.x) + "," + str(self.y) + "," + str(
 self.cost) + "," + str(self.parent_index)
 def planning(self, sx, sy, gx, gy):
  """
  dijkstra path search
  input:
s_x: start x position [m]
s_y: start y position [m]
gx: goal x position [m]
gx: goal x position [m]
  output:
rx: x position list of the final path
ry: y position list of the final path
  """
  start_node = self.Node(self.calc_xy_index(sx, self.min_x),
self.calc_xy_index(sy, self.min_y), 0.0, -1)
  goal_node = self.Node(self.calc_xy_index(gx, self.min_x),
  self.calc_xy_index(gy, self.min_y), 0.0, -1)
  open_set, closed_set = dict(), dict()
  open_set[self.calc_index(start_node)] = start_node
  while 1:
c_id = min(open_set, key=lambda o: open_set[o].cost)
current = open_set[c_id]
# show graph
if show_animation:  # pragma: no cover
 plt.plot(self.calc_position(current.x, self.min_x), self.calc_position(current.y, self.min_y), "xc")
 # for stopping simulation with the esc key.
 plt.gcf().canvas.mpl_connect(
  'key_release_event',
  lambda event: [exit(0) if event.key == 'escape' else None])
 if len(closed_set.keys()) % 10 == 0:
  plt.pause(0.001)
if current.x == goal_node.x and current.y == goal_node.y:
 print("Find goal")
 goal_node.parent_index = current.parent_index
 goal_node.cost = current.cost
 break
# Remove the item from the open set
del open_set[c_id]
# Add it to the closed set
closed_set[c_id] = current
# expand search grid based on motion model
for move_x, move_y, move_cost in self.motion:
 node = self.Node(current.x + move_x,
  current.y + move_y,
  current.cost + move_cost, c_id)
 n_id = self.calc_index(node)
 if n_id in closed_set:
  continue
 if not self.verify_node(node):
  continue
 if n_id not in open_set:
  open_set[n_id] = node  # Discover a new node
 else:
  if open_set[n_id].cost >= node.cost:# This path is the best until now. record it!open_set[n_id] = node
  rx, ry = self.calc_final_path(goal_node, closed_set)
  return rx, ry
 def calc_final_path(self, goal_node, closed_set):
  # generate final course
  rx, ry = [self.calc_position(goal_node.x, self.min_x)], [
self.calc_position(goal_node.y, self.min_y)]
  parent_index = goal_node.parent_index
  while parent_index != -1:
n = closed_set[parent_index]
rx.append(self.calc_position(n.x, self.min_x))
ry.append(self.calc_position(n.y, self.min_y))
parent_index = n.parent_index
  return rx, ry
 def calc_position(self, index, minp):
  pos = index * self.resolution + minp
  return pos
 def calc_xy_index(self, position, minp):
  return round((position - minp) / self.resolution)
 def calc_index(self, node):
  return (node.y - self.min_y) * self.x_width + (node.x - self.min_x)
 def verify_node(self, node):
  px = self.calc_position(node.x, self.min_x)
  py = self.calc_position(node.y, self.min_y)
  if px < self.min_x:
return False
  if py < self.min_y:
return False
  if px >= self.max_x:
return False
  if py >= self.max_y:
return False
  if self.obstacle_map[node.x][node.y]:
return False
  return True
 def calc_obstacle_map(self, ox, oy):
  self.min_x = round(min(ox))
  self.min_y = round(min(oy))
  self.max_x = round(max(ox))
  self.max_y = round(max(oy))
  print("min_x:", self.min_x)
  print("min_y:", self.min_y)
  print("max_x:", self.max_x)
  print("max_y:", self.max_y)
  self.x_width = round((self.max_x - self.min_x) / self.resolution)
  self.y_width = round((self.max_y - self.min_y) / self.resolution)
  print("x_width:", self.x_width)
  print("y_width:", self.y_width)
  # obstacle map generation
  self.obstacle_map = [[False for _ in range(self.y_width)]
 for _ in range(self.x_width)]
  for ix in range(self.x_width):
x = self.calc_position(ix, self.min_x)
for iy in range(self.y_width):
 y = self.calc_position(iy, self.min_y)
 for iox, ioy in zip(ox, oy):
  d = math.hypot(iox - x, ioy - y)
  if d <= self.robot_radius:self.obstacle_map[ix][iy] = Truebreak
 @staticmethod
 def get_motion_model():
  # dx, dy, cost
  motion = [[1, 0, 1],
[0, 1, 1],
[-1, 0, 1],
[0, -1, 1],
[-1, -1, math.sqrt(2)],
[-1, 1, math.sqrt(2)],
[1, -1, math.sqrt(2)],
[1, 1, math.sqrt(2)]]
  return motion

def main():
 print(__file__ + " start!!")
 # start and goal position
 sx = -5.0  # [m]
 sy = -5.0  # [m]
 gx = 50.0  # [m]
 gy = 50.0  # [m]
 grid_size = 2.0  # [m]
 robot_radius = 1.0  # [m]
 # set obstacle positions
 ox, oy = [], []
 for i in range(-10, 60):
  ox.append(i)
  oy.append(-10.0)
 for i in range(-10, 60):
  ox.append(60.0)
  oy.append(i)
 for i in range(-10, 61):
  ox.append(i)
  oy.append(60.0)
 for i in range(-10, 61):
  ox.append(-10.0)
  oy.append(i)
 for i in range(-10, 40):
  ox.append(20.0)
  oy.append(i)
 for i in range(0, 40):
  ox.append(40.0)
  oy.append(60.0 - i)
 if show_animation:  # pragma: no cover
  plt.plot(ox, oy, ".k")
  plt.plot(sx, sy, "og")
  plt.plot(gx, gy, "xb")
  plt.grid(True)
  plt.axis("equal")
 dijkstra = Dijkstra(ox, oy, grid_size, robot_radius)
 rx, ry = dijkstra.planning(sx, sy, gx, gy)
 if show_animation:  # pragma: no cover
  plt.plot(rx, ry, "-r")
  plt.pause(0.01)
  plt.show()

if __name__ == '__main__':
 main()

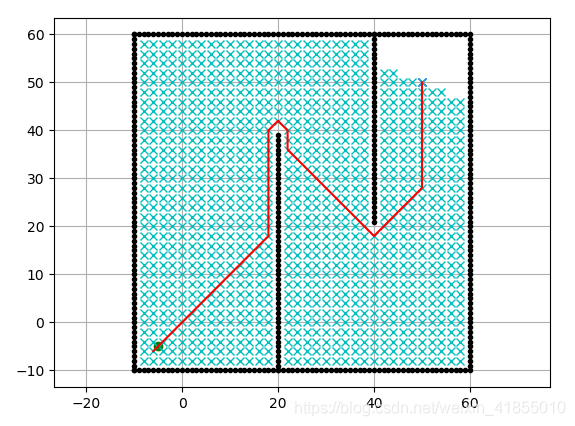
三、运行结果

四、 A*算法：Djikstra算法的改进

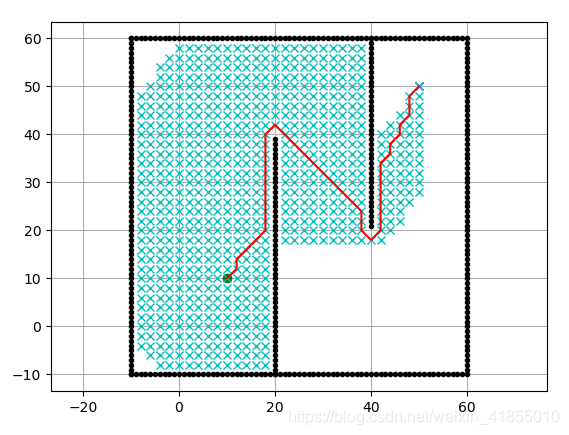
Dijkstra算法实际上是贪心搜索算法，算法复杂度为O( n 2 n^2 n2)，为了减少无效搜索的次数，我们可以增加一个启发式函数（heuristic），比如搜索点到终点目标的距离，在选择open_set元素的时候，我们将cost变成cost+heuristic，就可以给出搜索的方向性，这样就可以减少南辕北辙的情况。我们可以run一下PythonRobotics中的Astar代码，得到以下结果：