你知道怎么改进Python 二分法和牛顿迭代法求算术平方根吗(迭代法平方根)

二分法

def sqrtb(n):
 if n<0: raise ValueError('n>=0')
 left,right,x=0,n,n/2
 while not -1e-15<x*x-n<1e-15:
  if x*x>n:
right,x = x,left+(x-left)/2
  else:
left,x = x,right-(right-x)/2
 return x

求最接近算术平方根的整数

def sqrtB(x):
 if x==0: return 0
 #y,x=x,round(x)
 left,right,ret = 1,x,0
 while left<=right:
  mid = left + (right-left)//2
  if mid<x/mid:
left = mid+1
ret = mid
  elif mid==x/mid:
ret = mid
break
  else:
right = mid-1
 return ret

>>> sqrtB(9)
3
>>> sqrtB(8)
2
>>> sqrtB(9.2)
3.0
>>> sqrtB(7.8)
2.0
>>> sqrtB(4)
2
>>>

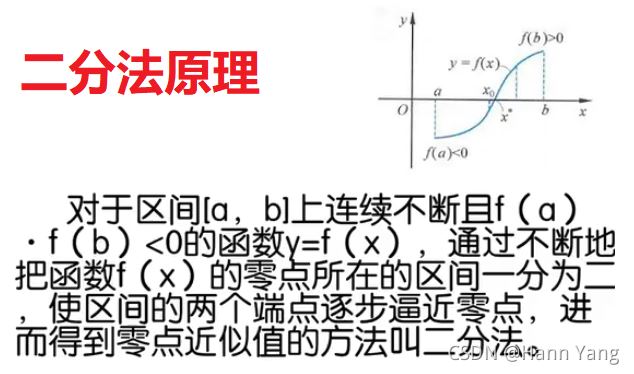
二分法原理

牛顿迭代法

def sqrtn(n):
 if n<0: raise ValueError('n>=0')
 x = n/2
 while not -1e-15<x*x-n<1e-15:
  x = (x+n/x)/2
 return x

一点小改进：不用1e-15来比较

def sqrt2(n):
 x = n
 while x*x>n:
  x = (x+n/x)/2
 return x

缺点：碰到n=7,13,...等，会进入死循环

增加判断跳出循环：

def sqrt(n):
 x = n
 while x*x>n:
  y,x = x,(x+n/x)/2
  if y==x: break
 return x

# sqrt(n) n=1~25的精度测试：

0.0
-2.220446049250313e-16
0.0
0.0
0.0
0.0
0.0
-4.440892098500626e-16
0.0
-4.440892098500626e-16
0.0
0.0
4.440892098500626e-16
0.0
0.0
0.0
0.0
8.881784197001252e-16
-8.881784197001252e-16
0.0
0.0
0.0
0.0
0.0
0.0
>>>

牛顿迭代法原理

从函数意义上理解：要求函数f(x)=x²，使f(x)=num的近似解，即x²-num=0的近似解。

从几何意义上理解：要求抛物线g(x)=x²-num与x轴交点（g(x)=0）最接近的点。

假设g(x0)=0，即x0是正解，让近似解x不断逼近x0，x0 ~ x - f(x)/f'(x)

def cubeN(n):
 x,y = n/3,0
 while not -1e-15<x-y<1e-15:
  y,x = x,(2/3)*x+n/(3*x*x)
 return x
'''
>>> cubeN(27)
3.0
>>> cubeN(9)
2.080083823051904
>>>
'''