Python数学建模StatsModels统计回归模型数据的准备(数据文件)

1、读取数据文件

回归分析问题所用的数据都是保存在数据文件中的，首先就要从数据文件读取数据。

数据文件的格式很多，最常用的是 .csv，.xls 和 .txt 文件，以及 sql 数据库文件的读取。

使用 pandas 从数据文件导入数据的程序最为简单，示例如下：

（1）读取 .csv 文件：

 df = pd.read_csv("./example.csv", engine="python", encoding="utf_8_sig")
 # engine="python"允许处理中文路径，encoding="utf_8_sig"允许读取中文数据

（2）读取 .xls 文件：

df = pd.read_excel("./example.xls", sheetname='Sheet1', header=0, encoding="utf_8_sig")
 # sheetname 表示读取的sheet，header=0 表示首行为标题行， encoding 表示编码方式

（3）读取 .txt 文件：

 df = pd.read_table("./example.txt", sep="\t", header=None)
 # sep 表示分隔符，header=None表示无标题行，第一行是数据

2、数据文件的拆分与合并

统计回归所需处理的数据量可能非常大，必要时需对文件进行拆分或合并，也可以用 pandas 进行处理，示例如下：

（1）将 Excel 文件分割为多个文件

 # 将 Excel 文件分割为多个文件
 import pandas as pd
 dfData = pd.read_excel('./example.xls', sheetname='Sheet1')
 nRow, nCol = dfData.shape  # 获取数据的行列
 # 假设数据共有198,000行，分割为 20个文件，每个文件 10,000行
 for i in range(0, int(nRow/10000)+1):
  saveData = dfData.iloc[i*10000+1:(i+1)*10000+1, :]  # 每隔 10,000
  fileName= './example_{}.xls'.format(str(i))
  saveData.to_excel(fileName, sheet_name = 'Sheet1', index = False)

（2）将多个 Excel 文件合并为一个文件

 # 将多个 Excel 文件合并为一个文件
 import pandas as pd
 ## 两个 Excel 文件合并
 #data1 = pd.read_excel('./example0.xls', sheetname='Sheet1')
 #data2 = pd.read_excel('./example1.xls', sheetname='Sheet1')
 #data = pd.concat([data1, data2])
 # 多个 Excel 文件合并
 dfData = pd.read_excel('./example0.xls', sheetname='Sheet1')
 for i in range(1, 20):
  fileName = './example_{}.xls'.format(str(i))
  dfNew = pd.read_excel(fileName)
  dfData = pd.concat([dfData, dfNew])
 dfData.to_excel('./example', index = False)
 # = 关注 Youcans，分享原创系列 https://blog.csdn.net/youcans =

3、数据的预处理

在实际工作中，在开始建立模型和拟合分析之前，还要对原始数据进行数据预处理（data preprocessing），主要包括：缺失值处理、重复数据处理、异常值处理、变量格式转换、训练集划分、数据的规范化、归一化等。

数据预处理的很多内容已经超出了 Statsmodels 的范围，在此只介绍最基本的方法：

（1）缺失数据的处理

导入的数据存在缺失是经常发生的，最简单的处理方式是删除缺失的数据行。使用 pandas 中的 .dropna() 删除含有缺失值的行或列，也可以对特定的列进行缺失值删除处理。

 dfNew = dfData.dropna(axis = 0))  # 删除含有缺失值的行

有时也会填充缺失值或替换缺失值，在此就不做介绍了。　

（2）重复数据的处理

对于重复数据，通常会删除重复行。使用 pandas 中的 .duplicated() 可以查询重复数据的内容，使用 .drop_duplicated() 可以删除重复数据，也可以对指定的数据列进行去重。

 dfNew = dfData.drop_duplicates(inplace=True)  # 删除重复的数据行

（3）异常值处理

数据中可能包括异常值，是指一个样本中的数值明显偏离样本集中其它样本的观测值，也称为离群点。异常值可以通过箱线图、正态分布图进行识别，也可以通过回归、聚类建模进行识别。

箱线图技术是利用数据的分位数识别其中的异常点。箱形图分析也超过本文的内容，不能详细介绍了。只能笼统地说通过观察箱形图，可以查看整体的异常情况，进而发现异常值。

 dfData.boxplot()  # 绘制箱形图

对于异常值通常不易直接删除，需要结合具体情况进行考虑和处理。使用 pandas 中的 .drop() 可以直接删除异常值数据行，或者使用判断条件来判定并删除异常值数据行。

 # 按行删除，drop() 默认 axis=0 按行删除
 dfNew = dfData.drop(labels=0)# 按照行号 labels，删除 行号为 0 的行
 dfNew = dfData.drop(index=dfData[dfData['A']==-1].index[0])# 按照条件检索，删除 dfData['A']=-1 的行

4、Python 例程（Statsmodels）

4.1 问题描述

数据文件中收集了 30个月本公司牙膏销售量、价格、广告费用及同期的市场均价。
　　（1）分析牙膏销售量与价格、广告投入之间的关系，建立数学模型；
　　（2）估计所建立数学模型的参数，进行统计分析；
　　（3）利用拟合模型，预测在不同价格和广告费用下的牙膏销售量。

本问题及数据来自：姜启源、谢金星，数学模型（第 3版），高等教育出版社。
需要说明的是，本文例程并不是问题最佳的求解方法和结果，只是使用该问题及数据示范读取数据文件和数据处理的方法。

4.2 Python 程序

# LinearRegression_v3.py
# v1.0: 调用 statsmodels 实现一元线性回归
# v2.0: 调用 statsmodels 实现多元线性回归
# v3.0: 从文件读取数据样本
# 日期：2021-05-06
# Copyright 2021 YouCans, XUPT
import numpy as np
import pandas as pd
import statsmodels.api as sm
import matplotlib.pyplot as plt
def main():
 # 读取数据文件
 readPath = "../data/toothpaste.csv"  # 数据文件的地址和文件名
 try:
  if (readPath[-4:] == ".csv"):
dfOpenFile = pd.read_csv(readPath, header=0, sep=",")  # 间隔符为逗号，首行为标题行
# dfOpenFile = pd.read_csv(filePath, header=None, sep=",")  # sep: 间隔符，无标题行
  elif (readPath[-4:] == ".xls") or (readPath[-5:] == ".xlsx"):  # sheet_name 默认为 0
dfOpenFile = pd.read_excel(readPath, header=0)  # 首行为标题行
# dfOpenFile = pd.read_excel(filePath, header=None)  # 无标题行
  elif (readPath[-4:] == ".dat"):  # sep: 间隔符，header：首行是否为标题行
dfOpenFile = pd.read_table(readPath, sep=" ", header=0)  # 间隔符为空格，首行为标题行
# dfOpenFile = pd.read_table(filePath,sep=",",header=None) # 间隔符为逗号，无标题行
  else:
print("不支持的文件格式。")
  print(dfOpenFile.head())
 except Exception as e:
  print("读取数据文件失败：{}".format(str(e)))
  return
 # 数据预处理
 dfData = dfOpenFile.dropna()  # 删除含有缺失值的数据
 print(dfData.dtypes)  # 查看 df 各列的数据类型
 print(dfData.shape)  # 查看 df 的行数和列数
 # colNameList = dfData.columns.tolist()  # 将 df 的列名转换为列表 list
 # print(colNameList)  # 查看列名列表 list
 # featureCols = ['price', 'average', 'advertise', 'difference']  # 筛选列，建立自变量列名 list
 # X = dfData[['price', 'average', 'advertise', 'difference']]  # 根据自变量列名 list，建立 自变量数据集
 # 准备建模数据：分析因变量 Y(sales) 与 自变量 x1~x4  的关系
 y = dfData.sales  # 根据因变量列名 list，建立 因变量数据集
 x0 = np.ones(dfData.shape[0])  # 截距列 x0=[1,...1]
 x1 = dfData.price  # 销售价格
 x2 = dfData.average  # 市场均价
 x3 = dfData.advertise  # 广告费
 x4 = dfData.difference  # 价格差，x4 = x1 - x2
 X = np.column_stack((x0,x1,x2,x3,x4))  #[x0,x1,x2,...,x4]
 # 建立模型与参数估计
 # Model 1：Y = b0 + b1*X1 + b2*X2 + b3*X3 + b4*X4 + e
 model = sm.OLS(y, X)  # 建立 OLS 模型
 results = model.fit()  # 返回模型拟合结果
 yFit = results.fittedvalues  # 模型拟合的 y 值
 print(results.summary())  # 输出回归分析的摘要
 print("\nOLS model: Y = b0 + b1*X + ... + bm*Xm")
 print('Parameters: ', results.params)  # 输出：拟合模型的系数
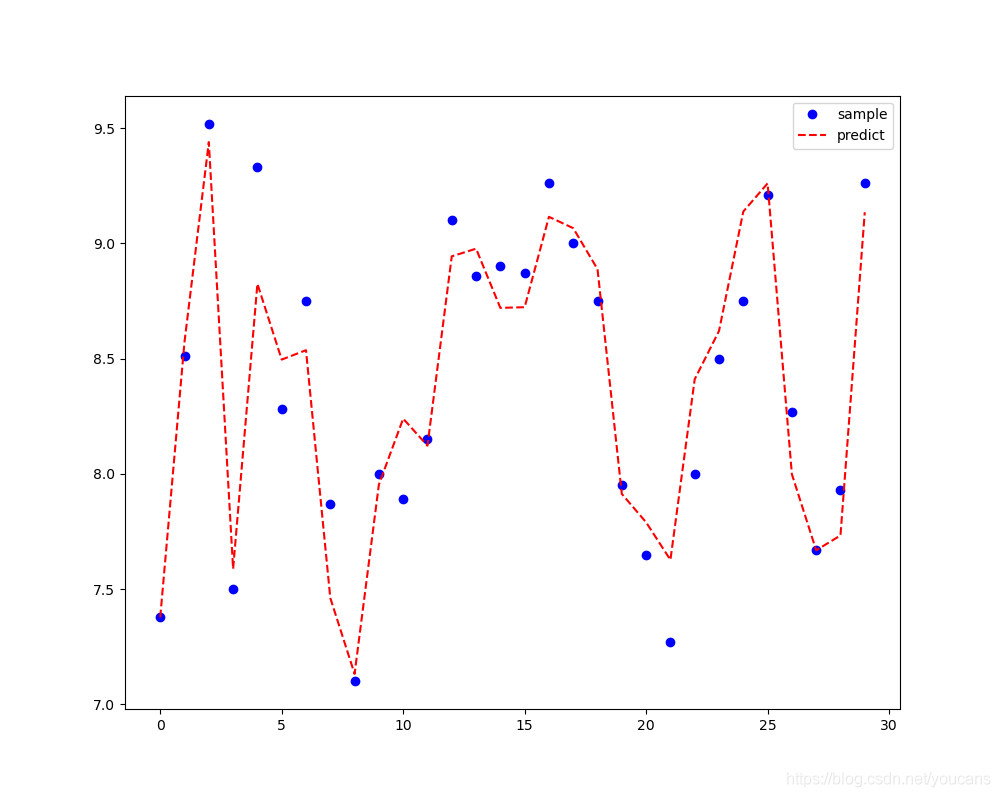
 # 拟合结果绘图
 fig, ax = plt.subplots(figsize=(10, 8))
 ax.plot(range(len(y)), y, 'bo', label='sample')
 ax.plot(range(len(yFit)), yFit, 'r--', label='predict')
 ax.legend(loc='best')  # 显示图例
 plt.show()  # YouCans, XUPT
 return
if __name__ == '__main__':
 main()

4.3 程序运行结果：

period  price  average  advertise  difference  sales
0 13.85  3.80 5.50 -0.057.38
1 23.75  4.00 6.75  0.258.51
2 33.70  4.30 7.25  0.609.52
3 43.70  3.70 5.50  0.007.50
4 53.60  3.85 7.00  0.259.33
OLS Regression Results
==============================================================================
Dep. Variable:salesR-squared:  0.895
Model:OLSAdj. R-squared:0.883
Method:  Least SquaresF-statistic:74.20
Date: Fri, 07 May 2021Prob (F-statistic):  7.12e-13
Time:11:51:52Log-Likelihood:  3.3225
No. Observations:30AIC: 1.355
Df Residuals: 26BIC: 6.960
Df Model:3 
Covariance Type:nonrobust 
==============================================================================
  coef std err tP>|t|[0.0250.975]
------------------------------------------------------------------------------
const 8.03682.4803.2410.003 2.94013.134
x1-1.11840.398  -2.8110.009-1.936-0.300
x2 0.26480.1991.3320.195-0.144 0.674
x3 0.49270.1253.9380.001 0.236 0.750
x4 1.38320.2884.7980.000 0.791 1.976
==============================================================================
Omnibus:0.141Durbin-Watson: 1.762
Prob(Omnibus):0.932Jarque-Bera (JB): 0.030
Skew:0.052Prob(JB):0.985
Kurtosis:  2.885Cond. No.2.68e+16
==============================================================================
OLS model: Y = b0 + b1*X + ... + bm*Xm
Parameters:  const 8.036813
x1-1.118418
x2 0.264789
x3 0.492728
x4 1.383207