Python 马氏距离求取函数详解(距离马氏)

马氏距离区别于欧式距离，如百度知道中所言：

马氏距离(Mahalanobis distance)是由印度统计学家马哈拉诺比斯(P. C. Mahalanobis)提出的，表示点与一个分布之间的距离。它是一种有效的计算两个未知样本集的相似度的方法。与欧氏距离不同的是，它考虑到各种特性之间的联系（例如：一条关于身高的信息会带来一条关于体重的信息，因为两者是有关联的），并且是尺度无关的(scale-invariant)，即独立于测量尺度。对于一个均值为μ，协方差矩阵为Σ的多变量向量，其马氏距离为sqrt( (x-μ)'Σ^(-1)(x-μ) )。

因此，对于马氏距离最终的定义式为：

上代码，将马氏距离求取式，封装为Python函数，拷贝即可使用：

from numpy import *
import numpy
def get_mahalanobis(x, i, j):
 xT = x.T  # 求转置
 D = numpy.cov(xT)  # 求协方差矩阵
 invD = numpy.linalg.inv(D)  # 协方差逆矩阵
 assert 0 <= i < x.shape[0], "点 1 索引超出样本范围。"
 assert -1 <= j < x.shape[0], "点 2 索引超出样本范围。"
 x_A = x[i]
 x_B = x.mean(axis=0) if j == -1 else x[j]
 tp = x_A - x_B
 return numpy.sqrt(dot(dot(tp, invD), tp.T))

使用方式如下：

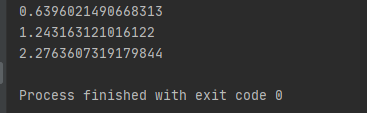
if __name__ == '__main__':
 # 初始化数据点集，或者从其它地方加载
 x = numpy.array([[3, 4], [5, 6], [2, 2], [8, 4]])
 # 求第0个点到均值之间的马氏距离（j为-1时代表均值）
 print(get_mahalanobis(x, 0, -1))
 # 求第0个点到第1个点之间的马氏距离
 print(get_mahalanobis(x, 0, 1))
 # 求第2个点到第3个点之间的马氏距离（索引从0开始算起）
 print(get_mahalanobis(x, 2, 3))

运行结果贴图